by Steve Bryson
There are many different of ways atarriving at the Lorentz Transformation. This is because theLorentz Transformation can be thought of as coming from any oneof the following equivalent statements:
•The speed of lightis the same for all observers
•Spacetime is a 4dimensional space with distance formula given by s2 =t2-x2
•Spacetime is a 4-dimensional hyperbolic space
The derivation from the first principlecan be found in Einstein's popular book on relativity (see booklist) as an appendix. This is the classical approach and requiresnothing more than a knowledge of algebra.
The derivation from the second principleis very easy and only requires a working knowledge of high schoolalgebra. This is presented in detail in this handout.
The third derivation is, I feel, thedeepest conceptually, but it requires knowledge of hyperbolictrigonometry. I give an introduction to this in this handout. Itis certainly the way I think about it.
The following will perhaps look prettyhard, but that is because I am going to show every step one stepat a time. I promise that for this section I will use nothing buthigh school algebra to get from one step to another, and I willdescribe the operation at each step.
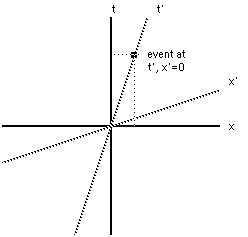
First, consider two coordinate systemsin relative motion with velocity v with coordinates t,x and t',x'and coinciding origins. Here the t,x system in defined asmotionless, and the t',x' system is in relative motion withvelocity v.
Look at an event with coordinates t', x'= 0:

If we are given the t' coordinates ofthe event (we know that the x' coordinate =0), how do we find thex and t coordinates of the event. We use the fact that thespacetime distance is independent of coordinates, which is to saythat the spacetime distance in the two coordinate systems is thesame.
The spacetime distance in this case is:
![]()
or
![]() .
.
Take square root of both sides:
![]()
Factor out a (ct)2:
![]()
![]()
but x/t = velocity v, so isolate thex/t:
![]()
![]()
![]()
Solve this for t and find that
![]()
This is the formula for the t coordinatein the case described above. Now x=vt (as v=x/t), so
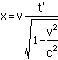
Thus the event at x'=0 and time t' willhave coordinates
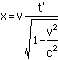
![]()
Thus something that happens at t'=2seconds in the moving coordinate system will happen at some tseconds (where t > 2seconds) in the nonmoving coordinatesystems. It will also have a non-zero x coordinate. Notice thateven though the point in the moving system had x' coordinate =0,there is a nonzero x coordinate for the event. This is becausethe Lorentz Transformation mixes the coordinate axes.
The more general case: Consider now anevent that has t' and x' coordinates both nonzero:
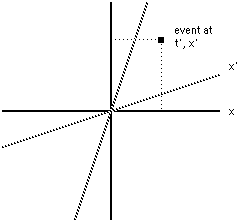
We ask the same question: What are the xand t coordinates of the event? We start by assuming that theLorentz transformation is linear in x' and t' as all goodrotations should be. This means that the transformation is of theform
t = Dt'+Ax'
x = Ct'+Bx'
What we need to do is determine what A,B,C and D are (we'll find that they are functions of velocity).But we already know what D and C are from the simpler case above,for they assumed that x'=0. Thus we know that the Lorentztransformation is of the form
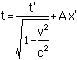
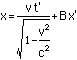
So now we need to find A and B. We dothis by again using the fact that the spacetime distance of theevent from the origin is the same in both coordinate systems:
c2t2-x2=c2t'2-x'2
First we compute c2t2-x2in the transformed coordinates: we substitute the above Lorentztransformation expressions for t and x into the spacetimedistance:
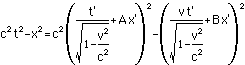
What we want to do with this is compareit with c2t'2-x'2. As it shouldbe equal, we will be able to determine A and B. We do this bypulling the x' and t' terms out of the above formula andcomparing coefficients. First we expand the squares:
Then collect the like terms:
Now factor out the terms with t' and x'in them:
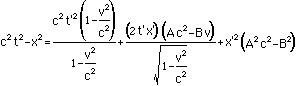
Simplify and note that this must beequal to c2t'2-x'2:
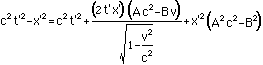
Now we demand that whatever multipliesthe t' on the left hand side of the equal sign is equal towhatever multiplies the t' on the right hand side of the equalsign. Similarly for the x' and the t'x' term. Thus there arethree cases:
t' case: we have c2multiplying the t' on both sides, so we do not learn anythinghere.
t'x' case: we have no t'x' term on theleft side at all, so whatever multiplies the t'x' term on theright side must be equal to zero:
![]()
We solve this for A in terms of B:
![]()
![]()
We will use this in a minute.
x' case: we have a -1 multiplying the x'on the left side, so whatever multiplies the x' on the right sidemust be equal to -1:
![]()
Now substitute the formula
![]()
And solve for B:
![]()
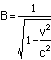
Now plug this back into the formula forA:
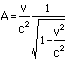
We now know A and B. We can plug thisinto our starting formulas for the Lorentz Transformation
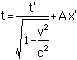
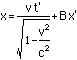
to get
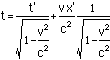
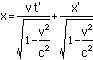
This is the complete Lorentztransformation. Note that if something has a length (x) of 1 inthe nonmoving coordinate system, then it's length in the movingcoordinate system (x') would be shorter. Note that even thoughfor a length there is no t part (t=0), there will be a t' partfrom the mixing of space and time by the Lorentz transformation.This would be seen as a small rotation of the object beingmeasured along an axis perpendicular to the direction of motionand the direction measured.