by Steve Bryson
The current success of quantum field theories describingvirtually all known elementary particle interactions is based ona particular type of field theory call a gauge theory.
A gauge theory is based on the recognition of a certain factthat is true in any quantum theory. This is that the only waythat a wave function can be observed is through the probabilitythat the wave function predicts, which is given by the strengthof the wave. Up until now we have been thinking of the wavefunction as a number at each point in space. In actuality, thewave function is somewhat more complicated. In the case of anelectron, the wave function is given in terms of two numbers (foryou techies out there the wave is complex valued). Now these twonumbers can be thought of as an arrow, not in our normalspacetime, but in another space that we envision attached tospacetime everywhere. The buzzword for this is 'fiber bundle', soI will call this new space the bundle space. Then the strength ofthe wave function becomes the length of the arrow. Now thecrucial observation of gauge theories is that in quantummechanics it is only the strength of the wave that counts (itgives the probabilities). If the wave is actually described by anarrow (as it is here), then it is only the length of the arrowthat counts and not its direction. In other words, we can neverknow what direction the arrow is pointing. Physicists call this a'gauge symmetry', as at each point of space the theory issymmetric under rotation of the arrow.
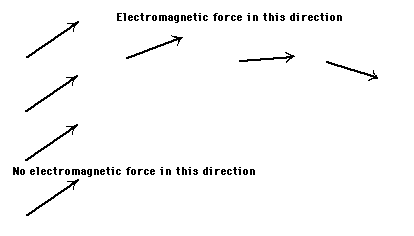
According to the mathematics of the theory, however, the wavefunction really is given by an arrow and so we cannot ignore itsdirection even though the direction cannot be observed. Inparticular, the arrow may be pointed in one direction at onepoint of normal space and if you move to another point in normalspace the arrow may rotate to point in another direction. Eventhough at each point you cannot observe the direction of thearrow, you do observe this rotation. It turns out that when youcreate a quantum field theory of just electrons (noelectromagnetic force yet) that respects and describes thisrotating of arrows this rotating of the arrows plays a role thatis identical to the role of the electromagnetic field in QED!Thus the electromagnetic force arises from the rotation of theelectron's wave function arrow as you move around in space.

I'll say this again a couple of different ways. According tothe natural quantum field theory of electrons, the electron'swave function is a little arrow (pointing into the bundle space)at each point of spacetime. Say that we move from one point toanother in spacetime. If the electron's wave function arrowrotated between the points we would experience that rotation asan electromagnetic force in spacetime. If we traveled to anotherpoint such that the arrows did not rotate, then we wouldexperience no electromagnetic force between those two points:
A more abstract and geometrical approach is the following.Instead of presuming that for some reason the electron's wavefunction arrows were not all aligned, make the equivalentpresumption that the bundle space where the arrows point iscurved. This means that when all the arrows are aligned in thecurved bundle space, they will appear to be rotated from theperspective of observers in spacetime. Then in the same way asabove we would experience that rotation as an electromagneticforce. The beauty of this view is that if one considers anelectron moving in the total space (spacetime + bundle space),then one can show that if the bundle space is curved an electronmoving in a straight line in the total space appears to move in acurved path in spacetime. The equations for this curved path thatyou get from this approach are exactly the equations describingthe path of a particle under the influence of a classicalelectromagnetic force. In this way we see the electromagneticforce as not a force at all, but as the manifestation of'straightest line' motion in a curved total space. (In this wayelectromagnetism becomes precisely analogous to gravity as thecurving of spacetime.)
Thus QED is the simplest gauge theory, and in fact this gaugeaspect of QED is crucial in proving that QED is renormalizable.
Once you understand electron wave functions as arrows in a twodimensional bundle space (that is described by two numbers), youcan ask if you can have wave functions in bundle spaces of higherdimensions! It turns out that quarks are correctly described by awave function that is described by an arrow that points into asix-dimensional bundle space (that is described by six numbers).It is said that quarks come in three 'colors', each colorlabeling two of the six directions, and the resulting gaugetheory is called Quantum Chromodynamics or QCD. (The three colorsare not to be confused with the flavors of quarks, called up,down, etc.. Each flavor comes in three colors, that is eachflavor is described by a six dimensional arrow.) So physicistsplay the same game that they did for QED as a gauge theory exceptnow the bundle space is six dimensional rather than two. Bypresuming that the direction of the six dimensional quark wavearrow is unobservable while the rotations of that arrow areobservable, we derive a QCD force between quarks (and onlybetween quarks) that can be viewed as the curvature of the sixdimensional bundle space. The rotation of the six dimensionalarrow is characterized by eight quantities called gluons.
It turns out that because this bundle space is sixdimensional, using renormalization techniques we discover thatthe strength of the force found in this way between quarksdepends on the separation of the quarks. Two quarks very closetogether act as if there is no force at all between them while ifthe quarks try to move apart the force gets stronger andstronger. Thus two quarks can never move far apart as the forcebetween them gets infinitely strong as they try to move apart.Thus the only things that can move apart from one another arethings that are not represented by arrows in this six dimensionalbundle space and so do not generate a force. Such objects areelectron type particles and certain groups of quarks (where thequark arrows in some sense cancel). Thus quarks can only exist inthe world as certain groups (which we call protons, neutrons,etc.) and never by themselves. This is called 'quark confinement'and is currently understood as coming from the fast that this sixdimensional bundle force gets stronger with increasing distance(called ''asymptotic freedom' due to the fact that short distancecorresponds to high energy). While it turns out that it is veryhard to make specific predictions in QCD, those that have beenmade match very well with observations, especially the actualobservation of asymptotic freedom at SLAC in Stanford in 1969.
While these gauge theories were successful in explaining theinteraction of matter and light (QED) and the behavior of quarks(QCD), there was still one force that acts on elementaryparticles that did not fit into a symmetric gauge theory. This isthe weak nuclear force which actually does not look much like aforce at all but shows up in the radioactive decay of atomicnuclei. To create a gauge theory of the weak force, physicistshad to drop the assumption that it is only strength of the wavefunction arrow describing a particle that counts. They had toallow the direction of the wave arrow to become directlyobservable. In addition, to make the theory work, the physicistshad to incorporate electromagnetism with the weak force in asingle gauge theory. What resulted was the first unified quantumfiled theory that both describes electromagnetism and the weaknuclear force. This theory is called 'the electroweak theory' orthe Glashow-Weinberg-Salam model after its prime inventors.
This theory has several remarkable features that I can onlybriefly mention here. First, the wave function arrow forparticles in this theory is described by four numbers and so isin a four dimensional bundle space. Now, however, the directionof the arrow is directly observable. Two of the directions in thebundle space correspond to the two directions of the electronwave function, and the other two correspond to the two directionsof the wave function for a particle called a neutrino. Thus whenthe wave function points in one direction we may see an electronwhile if it points in another direction we would see a neutrino.The rotating of this four dimensional wave arrow from point topoint in normal space is experienced as a combination of the weakand electromagnetic force. This rotation of the arrows isdescribed by four quantities called the photon (for theelectromagnetic part), W+, W-, and Z0(for the weak part). The force of this theory gets stronger withdistance (like QCD), but not as strong as QCD.
This theory actually starts with all particles massless. Whenbuilding the theory you assume that electrons, quarks, and so ondo not have any mass. The mass then arises by the mechanism thatallows the direction of the wave arrow to become detectable.Though in the current form you have to be very clever andconstruct your theory just right to explain all the masses, wehave for the first time some explanation for the existence ofmass. This explanation is, however, at a very primitive andunnatural level.
What is predicted, however, is that the W and Z quantitiesbehave like particles with a certain mass, and they were observedto actually have that mass at CERN in Europe in 1983. This is aspectacular confirmation of the electroweak theory.
The electroweak theory is founded on a mathematicalconstruction called spontaneous symmetry breaking or SSB. This isa rather artificial and ad hoc mechanism, however. Yet in usingit we are certainly doing something right. Taken at face value,the form of the SSB that works predicts an as yet unseen massiveparticle called the Higgs boson which plays a major role ingenerating the SSB. The fact that this particle has not yet beenseen is not a problem, as the electroweak theory makes nopredictions whatsoever about the properties of the Higgs. Inparticular it may be so heavy that we have not been able toproduce it yet. There are also theoretical reasons to think thatthe Higgs does not actually exist and the mechanism of SSB is notyet understood completely. There has been considerable effort tounderstand SSB in a more natural way (called technicolortheories), but so far there has been no success.
Inspired by the success of the electroweak model, since 1974several physicists were lead to postulate that the wave functionsof particles actually pointed into a higher dimensional bundlespace and all the particles we see correspond to differentdirections in that space. Several theories were written down, allof then using one form or another of the spontaneous symmetrybreaking mechanism. Currently there is no observational evidencefavoring or discrediting any one over the others, but here I willdescribe the simplest one so you can get some feel for what thesetheories look like.
This theory is called 'The minimal SU(5) model'. Here it ispostulated that the wave function arrow points into a 10dimensional bundle space, where six of the directions correspondto the quark color directions, two directions correspond to theelectron directions, and the last two correspond to the neutrinodirections. As the gauge symmetry is broken, these directionsactually look different to observers in spacetime, and thatdifference appears as quarks vs. electrons vs. neutrinos. Therotations of this ten dimensional wave arrow are described by 24quantities, 8 of which are the gluons, three are the W+,W-, and Z0, one is the photon, six of thenew ones are labels X and the last six are labeled Y.
This theory has reproduced all the predictions of theelectroweak theory and QCD. In addition, this theory predictsthat the X and Y quantities act like particles of a very largemass. Also, because now the ten dimensional wave can rotate frompointing in a quark direction to pointing in an electrondirection (for example), we can have quarks turning intoelectrons. Thus as a proton is made out of quarks, we expect tosee protons decaying into other particles. This theory predictsthat a proton should decay, on the average, in about 1031 years.This has not yet been seen, which is something of a problem forthe SU(5) model, but has not yet ruled it out. This theory alsopredicts that the electrical charge of quarks should be 1/3 thatof the electron, in accord with observation. There are also sometechnical predictions that match well with observation.
There are many other models built along these lines, but it iscurrently beyond the range of particle accelerators to test theirspecial predictions.
Another approach to the wave function:
The Feynman Path Integral
There is a new approach to quantum mechanics due to RichardFeynman that is rapidly taking over in research in quantum fieldtheory. Here I want to give a brief and simple description ofthis approach.
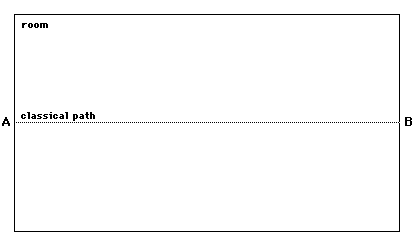
Feynman starts by saying that there is no wave function,rather what is strange about the world and gives rise to the waveaspects of nature is that motion is not what you think it is.Consider an electron moving from one end of the room to another,saying that it started at some particular place and ended atanother place. Label the starting point A and the ending point B.Classically, in the absence of any forces, the electron wouldtravel in a straight line, the straight line from A to B:
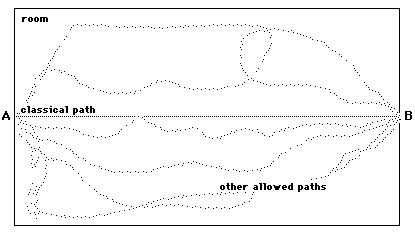
Feynman says "no, actually the electron traveled alongevery conceivable path starting at A and ending at B at the sametime." That is, the electron did not travel in any sensealong any particular path, but rather was somehow everywhere atonce (even though it is still a particle):
Then Feynman says that there is associated with this particlea quantity called an amplitude which is given by adding up allthe particle paths (whatever that means) with each term in thesum of particle paths multiplied by a weight function (amathematical term). Thus each term in the sum looks like
(weight function) times (path)
And the amplitude of the particle looks like
amplitude = sum of [(weight function) times (path)] added upover all paths
This amplitude is called the Feynman path integral.
All the physics is contained in the weight function, and it isdesigned so that the paths that are radically different from theclassical straight line will, on the average, cancel each otherout in the sum that gives the amplitude. This cancellationbecomes less and less likely for paths closer and closer to theclassical straight line path.
Then Feynman discovered that this amplitude with this specialweight function behaves exactly like the wave function oforthodox quantum mechanics. In this way Feynman derived the wavefunction of quantum mechanics by taking a radically differentview of motion.
The significance of this amplitude is that when we look tofind the electron at a particular point, the probability that wewill find the electron at that point is given by the magnitude ofthe amplitude. Thus in the above example where the electron ismoving from point A to point B, the amplitude along the classicalstraight line is very large so it is likely that we will find theparticle traveling along the classical straight line. Far fromthe classical path, the amplitude is small (though not zero) dueto the average cancellation, so it is unlikely that we will seethe particle there (though there is some chance):
While all this is very pretty and somewhat compelling as anunderstanding of how quantum phenomena arise, it should be keptin mind that the construction of the weight function is veryartificial and ad hoc (though not any more so than orthodoxquantum theory). It would be very nice to motivate this weightfunction as then we would have some understanding of why quantummechanics is true. Currently, the closest we are to this is theobservation that the Feynman path integral arises naturally whenasking questions about random processes in general mathematics(the field of stochastic calculus). Perhaps this implies that atsome level the universe is truly random. This is a very new areaof research.
The Path Integral in Quantum Field Theory
In describing the collision of two electrons, one starts withthe two electrons widely separated and therefore not (forpractical purposes) interacting and asks what are the chancesthat after the collision one will find two electrons widelyseparated and not interacting. In terms of the wave function, oneasks how one performs a transition from one wave describing twoelectrons through a wave describing a collision to a wavedescribing two electrons. Feynman says that one should considerall possible waves that look like the wave of two electrons inthe distant past and also look like the wave for two electrons inthe distant future, and can look like anything in between. Thenthe amplitude for getting two electrons, widely separated, out ofthe collision is given by the weighted sum (or Feynman pathintegral) over all these waves. Thus the probability for such aprocess is 'simply' given by calculating this sum. You can alsoask what is the probability of starting with two electrons andending up with two muons (or two quarks or anything else allowedby certain conservation laws). Then you would look at a wave thatstarts as a wave for two electrons and ends as a wave for twomuons. Then the sum in the amplitude for getting the muons out.The problem is that no one knows how to figure out what this sumis exactly. The best anyone can currently do is use anapproximation scheme.
This is where the difficulties of quantum field theory arise.In this approximation scheme, one expresses the Feynman pathintegral as new sum reflecting better and better approximationsto the actual answer. It looks something like this:
Feynman sum is approximately = A + B + C + ...
Here the letters stand for the approximate terms. It turns outthat these approximate terms can be expressed as diagrams oflines that can be usefully thought of as representing particlesand particle processes. These are the Feynman Diagrams discussedin last week's notes. I feel, however, that as these diagrams areexpressions for a mathematical approximation series they shouldnot be taken as representing anything in the structure of theworld.
Now the problem is that the first few approximation terms (Aand B and sometimes C) turn out to be infinite when you calculatethem. This is bad as no probability can be infinite (whensomething happens with certainty we say that it has a probability= 1 and something cannot have a higher probability than that!).It turns out that it is possible to eliminate these infinities bya clever redefinition of the weight function of the Feynman sum.This is called renormalization.
Many physicists are uncomfortable with renormalization as itinvolves cavalierly throwing about infinities as if they werenormal numbers. In the case of the quantum field theory of theinteraction of electromagnetism and matter (QuantumElectrodynamics or QED), however, the answers that you get afterrenormalizing match observations to the current limit of accuracy(currently about one part in a million!). Thus at least in QED wemust be doing something right. Also, recent work in simplernonphysical models of field theories have shown that even thoughthe approximation scheme in these models give infinities (justlike in QED), the actual total sum is finite. In other words ifwe could calculate what the sum is we would get a finite answer.Thus the infinities arising out of the approximation scheme camefrom the approximation scheme and not from the Feynman sum, atleast in these simpler models. The hope is that this is true forall actual quantum field theories.
Even though this approximation scheme and its requiredrenormalization are somewhat funky, they do predict a rathersurprising result. That is that the strength of the forcesdescribed by the theories is not constant but is a function ofthe energy of the system. In QED, for example, the strength ofthe electromagnetic force actually increases with energy veryslowly. Thus a magnet at very high temperatures (higher than thecenter of the sun to be noticeable) is stronger than a magnet inour room. In the case of the strong nuclear force, the forceactually gets weaker with higher energies, and seems to getinfinitely strong (a real infinity this time) for lower and lowerenergies. This is called 'asymptotic freedom' as it predicts thatfor very high energies we should see something like free quarks(this was observed at SLAC in 1969) and is used to explain whyyou can never see free quarks at everyday energies. This is aspectacular vindication of the quantum field theory approach.