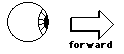
by Steve Bryson
We are going to be developing a new viewof the world. This new view is founded on the idea that space andtime combine to form a four dimensional space that we callspacetime. Before we can do this we need to know what a space is.
The word 'space' is used many differentways in our culture. We speak of empty space, outer space,parking space, and breathing space. If you are from Californiayou may speak of your own personal space and your mind space. Themathematician speaks of abstract spaces while the physicistspeaks of configuration spaces. All of these uses of the word'space' refer to very different things. All of these uses of theword space are completely valid.
Of all the above uses of the word'space', the use that is closest to the one we shall use isperhaps 'parking space'. It is the place where something happens,namely the parking of a car. It is sometimes empty and sometimesfull. Kids can play catch in this space. The space can haveproperties, like parking regulations, that effect what happens inthe space.
In this book, the word space will denotethe setting of our world. It is where things happen. People oftenpicture space by picturing an empty container. In this picture,space is, in some sense, what is left over if you removeeverything. In the way that I am using the word 'space', this ispartly right and partly misleading. It is right in that it showsspace to be the background in which things move. It is misleadingin that the space that I am referring to is not defined by somecontainer. The space I am talking about is the setting for theentire world. This picture is also misleading because the emptyspace is seen to be a passive background in which things happen.We shall see that the space in which everything sits can be avery active participant in what happens in that space.
So what are you supposed to picture whenI say space? Think this: Space is the place where things are.This is not a complete definition, but it is enough to getstarted. We will be getting more precise as we go on. The fullerpicture will come as we journey into different kinds of spaces.
A simple example of the kind of spacethat we will be talking about is called for. Allow me to presentyou with a simple hand held space: The page that these words arewritten on. If you look above where you are reading you will seethat the space contains many many black marks. For contrast, hereis some of the space without any marks, some empty space:
You can, if you wish, put more darkmarkings in this space. If you are ambitious you can even makemarkings that move around.
Now what about everything else, likeyour nose or the streetlight outside my window? Are these thingsin this paper space? No! Only those things on the paper are inthe space of this sheet of paper.
How about another example? A differentspace is the room that you are now in (this may be a very bigspace indeed if you are outside). Look around you and name someof the things that are in this space. Things can move in thisspace. You can throw this book across the room, you can observesome creature navigating about, you can even move in this spaceyourself!
This brings us to the next concept thatwe must get clear about. What does it mean to move in a space?This is not hard to understand, as we certainly know what it isto move around the room. We need to be precise about thisintuition so that we can talk of motion in other spaces. Motionis simply change of position in a space (we will worry aboutmaking the concept of position precise later). You move by goingfrom one place to another in a space. If this is too vague foryou, it is enough now to think this: motion is going from whereyou were to where you are.
When you move, you move in a particulardirection. How many possible directions can you move in?Infinitely many! You can move forward, sideways, up, and anycombination of these three. In the example space of the sheet ofpaper, a point could also move infinitely many directions,towards the sides of the paper, towards the top, or anycombination of the two.
In both the space of your room and thespace of the paper there is an infinity of possible directions ofmotion. Yet your intuition probably says that you have moredirections to move in you room than a point has on the sheet ofpaper. This intuition is correct, and understanding thisintuition in a precise way brings us to what is one of the mostimportant property of a space.
In the space of your room, you canchoose from an infinity of directions in which to move. Pictureyourself now choosing one of those directions. Turn to face inthat direction and start to move forward. As you move forward,notice that you are not moving sideways -- that is you are notmoving to your right or to your left, at least if you followed myinstructions. Notice also that you are not moving up or down.Your nose stays (more or less) at the same altitude from thefloor. This should not surprise you as, after all, this is whatit means to move forward! But now imagine a direction which issome combination of forward and left. You might point it out byraising your arm in that direction. Now ask yourself "am Imoving in the direction of a little bit forward and a little bitleft?" You are not moving exactly in that direction, but youare moving a little bit in that direction, as that direction is acombination of forward and left and you are moving forward. Nowtry to picture other such combinations of forward and sideways orforward and up and down. You are moving a little bit in all thesedirections if you are moving forward. (Something to think about:are you moving in a direction which is a combination of sidewaysand up and down only?) However, when you are moving forward youare not moving at all sideways or up and down. Close your eyes,get a good picture of this, and go on.
Now let's pretend we live in the paperspace. So that we have a concept of forward in this paper world,let's pretend that we look like a circle with one eye.
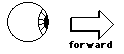
When we move in the direction that theeye is pointing, we say that we are going forward. Now when weare going forward, we are not going to our right or left, justlike walking around in our room.
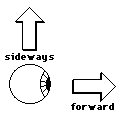
Just like in the space of our room, wecan choose a direction which is a combination of forward andsideways. When we are moving forward, we are moving a little bitin this new direction. There is one thing about this situationthat is different, though, and that is that there is no up anddown in the paper world. There is only forwards and sideways.
This is the essential difference betweenthe paper space and the space of your room. In your room when youwere moving forward there were two directions that you were notmoving in: sideways and up and down. In the paper space, when youmove forward, there is only one direction that you do not movein: sideways. This is because the space of your room is a threedimensional space and the space of the paper is a two dimensionalspace. The idea here is that a space has some special directions.These directions are special in that if you move along one ofthese directions you do not move along any of the otherdirections. The dimension of a space is the number of thesespecial directions. Here is the definition of the dimension of aspace:
The dimension of a space is the numberof directions in that space so that if you move along one ofthese special directions you do not move along any of the otherspecial directions.
There is one subtlety here. Thedimension of a space counts the number of directions that arespecial in the way described above. In the space of your room,that number is three and in the space of the paper that number istwo. This just means that, in the space of your room, there arethree special directions. Nothing says which three directionsthey are. After all, you choose what forward is. Once you choosewhat direction forward will be, then the other two specialdirections are fixed. They are sideways (to your left and right)and up and down. It is important to understand that you choosethe three special directions by choosing one of them. If you arelying in bed, the your forward would be towards the ceiling, yoursideways is to your left and right, and your up and down is alongthe length of the bed. To say a space is three dimensional is tosay that there three special directions of motion--not whichthree directions they are.
Why do we care about the dimension of aspace? The real answer is that by understanding the dimension ofa space we get deep understanding of how things are in thatspace. This is very abstract, however. Is there not a moretangible excuse for understanding dimension than this?
Of course there is! We need to know thenumber of dimensions of a space in order to locate objects inthat space. Consider yourself in the space of your room. Holdingvery still, picture a point in space about two feet in front ofyour nose. How would you tell your cleaning person, who will beworking tomorrow while you are away, where that spot in space isso that he can make sure that it is not dirty? Think about thisproblem a little before you go on. There are actually many waysto specify where the spot is in space. The most natural way is tosay that the spot is so far from the floor, so far from thiswall, and so far from this side wall. Notice that you neededthree numbers to tell where this point is. You may specify thepoint by saying something like "It is two feet in front ofme." This seems to only use two numbers (distance anddirection). Actually, however, for this to work you need tospecify your position in space as well, and that will take threenumbers. You can be very clever and try to come up with otherways to specify the position of that point in this space. If youdo this correctly, you will find that you will always need threenumbers!
This is no coincidence. The need forthree numbers in the space of your room is intimately bound withthe fact that your room is three dimensional. This means thatthere are three directions that do not effect each other -- thesedirections are independent. The dimension of a space measures thenumber of independent directions in that space. If you try toindicate the position of a point in a three dimensional spacewith only two numbers, you are fixing only two of theseindependent directions. This leaves no information about thethird, and the position of the point can be anywhere along thatthird direction. Topology, a very pretty and pictorial branch ofmathematics, concerns itself in part with this extra freedom ofposition in abstract spaces. For our purposes, however, we aregoing to demand that we specify the position of an object inspace completely. This means that in a three dimensional space wewill need three numbers.
What about in the two dimensional spaceof this paper? Let's start over again in the context of thisexample. How would specify the position of the following dot inthis paper space?
.
The most obvious way is to say that itis such a distance from the top of the page and such a distancefrom the left side. Or it could have been from the bottom andfrom the right side, or any combination of these. The main thingto notice here is that two numbers do it. There are other ways tospecify the position of that point, and you may wish to amuseyourself by trying to picture them. All of them will take atleast two numbers to do the job (of course, you can invent waysthat take more than two numbers, by using each dimension morethan once). This is because the space of the paper is twodimensional.
When you are specifying the position ofa point in a way that uses the smallest number of numbers, thesenumbers are called the coordinates of the point. Thus in thespace of the paper you will need two coordinates to specify aposition. In the space of your room you will need threecoordinates to specify the position of a point.
How does the motion of objects in spaceappear in terms of coordinates? Very simple! The coordinates ofsomething that is moving in a space change as the somethingmoves. Thus motion is simply the changing of coordinates.
Coordinates are tremendously importantif you are going to attempt to make a precise description ofnature. Physicists wish to describe objects in the universe,measure their motion and by so doing come to some understandingof how the universe is put together. In order to do this, theymust use coordinates to make precise, simple statements aboutwhat the objects in the universe are doing. Without this, itwould be very hard to see patterns in the behavior of objects,and without patterns it would be very hard to understand how theuniverse works.
But wait! How can coordinates be soimportant? After all, the coordinates we use to describe ourspaces are entirely made up by us, and we could as easily as nothave made up another set of coordinates for our description! Thisis a very important point to understand. We impose our owncoordinate systems on nature. This does not mean that there is noindependent nature out there that we are observing (ignoring fornow the current controversies around quantum mechanics). It doesmean that if we measure something, then for it to be actuallypart of nature, as opposed to some artifact of our measuringprocess, we had better find that this measurement has the samevalue in all coordinate systems. It is a wonderful and somewhatsurprising fact that there are things in nature that satisfythis. Relativity theory is about finding those aspects ofspacetime that are independent of what coordinates we use tomeasure them.