by Steve Bryson
For the purposes of this course, we willthink of a space as the background in which things move (likebaseballs). We experience walking around in a three-dimensionalspace. That means that we can go any of three directions (up,forward, or sideways), either one at a time or in anycombination. These three directions are special, in that if yougo exactly along one, you do not go along any of the others.Think this: If you go forward, you do not go up or sideways (andif you go sideways....). The number of directions (in thespace) that have this special property is called the dimension ofthe space. Remember- the dimension of a space is a number, not adirection. You may wish to entertain yourself by trying toimagine more than three directions with this property. If yousucceed, you are not visualizing something properly. Rememberthat if you move along one direction you are moving along theopposite direction with a negative speed. This is why forwardsand backwards are not different special directions.
Following textbooks from grammar schoolon up, we will name these three special directions x, y, and z.(I think of them as: x is sideways; y is up and down; z is frontand back).
All of this is much easier to see if,instead of thinking in three dimensions, we think in terms oftwo. This is like saying "I will only move forwards andbackwards (one dimension) and side to side (another dimension),but I will not move up or down (this is the missing thirddimension)". This makes it much easier for me to makediagrams of what I am talking about, as the paper you are holdingis two dimensional. Because I am writing these notes (and it isimportant to understand that there is no better reason), I willchoose the x and y directions. I will then represent them withtwo perpendicular lines called the x axis and the y axis:
In future figures, the axes will bedenoted by the letter naming the direction, dropping the wordaxis: x axis will become x, etc..
What is the significance of these axes?They can be used to indicate the position of an object in ourspace. The kinds of objects we will be talking about for the nearfuture will be points on the paper. Using the axes, we canindicate the positions of points in the following way. First,call where the two axes meet the center or origin (I willundoubtedly unconsciously interchange them). Then say how far youhave to travel along the x axis from the center (in your favoriteunit of measurement) until you are directly under the desiredpoint. Finally say how far you have to travel along the y axisfrom the center until you are exactly beside the point:
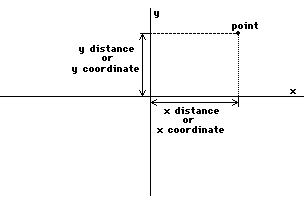
Once you know where the center is, youonly need two numbers to indicate the position of the point.These numbers are called the coordinates of the point. Of course,it is no coincidence that you need two numbers in a twodimensional space. In fact the simplest way to give the positionis in terms of the directions used to define the dimension(though you do not have to do this (why?)).
What would the path of a point look likeif it were moving? It would look like a line! It would be astraight line if the point did not turn, and it would look like awiggly line if it did:
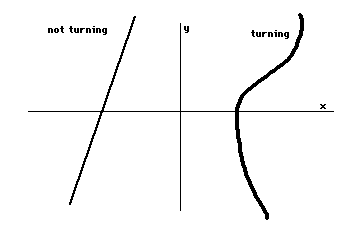
If you are having trouble visualizingwhere these lines come from, picture the above figure as a mapand the lines are the paths of cars (here the cars correspond tothe points and the lines correspond to the roads).
We are now well equipped for thinkingand visualizing spaces, especially when we can ignore all but twodimensions of the space. We can now, therefore, turn to thinkingabout adding time to our space.
When we want to find something, we needto know not only where it is, but also when it'sthere. Thus in addition to the three numbers needed to locateposition in our three dimensional world, we need a fourthnumber--time. We thus need four coordinates to locate somethingin our world. This gives us the clever idea of treating time as adirection that gives us a fourth dimension! Let's see ifthis works.
Think of yourself as moving throughtime, not worrying about whether or not this means anything.Stand still, close your eyes, and feel the motion through time.Are you moving in space? Not if you obeyed my instruction tostand still! So if time is thought of as a direction, it is adirection that you can move along without moving in any of thethree spatial directions! It thus defines a fourth dimension! Ifall this seems too simple to you, you are catching on. It issimple, once we are clear about what we mean by dimension!
Now does this mean anything? What can wemean by saying that we are moving through time? Motion is changein position. If we think of time as a fourth coordinate, then thevalue of this coordinate certainly changes--in fact we cannotstop it from changing! We cannot stop time, though many havetried! In this sense we are certainly always moving through time.The time coordinate always changes. In this class we are going tocombine the observation that we move through time with theobservation that the direction we move in time seems to define afourth dimension. We are going to find that taking this viewpointleads us to a picture of reality that makes the results ofrelativity theory very natural. This, to me, says that this ideaof motion through time means quite a lot.
Enough philosophy. What we have arrivedat is that the space we live in is actually four dimensional.This does not mean that all four dimensions are alike.There is something very special about the time dimension. This isreflected in the fact that you cannot stop moving through time,though you can stand still with respect to the three other(spatial) dimensions. We will never come to understand whytime is different (no one does), but we will, by carefullyexamining this difference, understand many deep facts about ourworld.
We start by trying to visualize our fourdimensional world. There is immediately a problem. This world isfour dimensional and we only know how to visualize in (at most)three dimensions. What to do? We will have to somehow reduce thenumber of dimensions that we are trying to visualize!
The space part of spacetime is threedimensional. It is a fortunate fact that the three spatialdirections are completely equivalent. If we know one, we know theothers. We can thus forget one of the spatial directions (let'sdrop the z direction), and reduce our problem to trying tovisualize a three dimensional spacetime, with a time directionand two spatial directions. We have succeeded in making the worldpossible to visualize. However, not everybody finds it easy tovisualize things in three dimensions. But wait! We still have atwo dimensional spatial part, and these two spatial directionsare equivalent. For your sake and for the sake of my drawingslet's drop another spatial direction (the y direction). We arenow left with a two dimensional spacetime with the timedirection, denoted by t, and the x direction:
This is a spacetime diagram. We will beseeing a lot of this.
This diagram allows us to see motion inthe x and t directions only. This is the same as saying that Iwill only move sideways (in the x direction) and, unavoidably, inthe time direction.
What is a point in our spacetimediagram? It is something with two coordinates, a value for x anda value for t. So it is something that happened in a particular placeat a particular time. This is called an event. Events arethe points on a spacetime diagram. Examples of events are: a bathitting a ball, a hand clap, or a firecracker going off. Notethat these examples are not exactly events, as they take a(very short) amount of time to occur, but they are the closestthat everyday things come.
What does an object in the real worldlook like on our spacetime diagram? Since we only have onespatial dimension, think about a very thin rod. Idealize this rodas a one dimensional object. Put the end of the rod at the centerof the diagram. As time goes by, the rod will sweep out an areaon the spacetime diagram, for it is not moving in space but ismoving in time. Thus an object in the real world looks like acollection of events on our spacetime diagram:
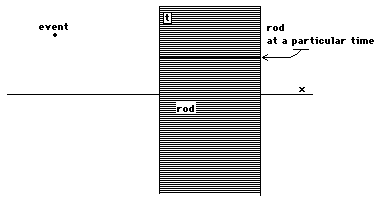
The rod, which we idealize as a onedimensional object in space is (unavoidably) a two dimensionalobject in spacetime. You can think of this in several ways. Ithink of the rod as 'sweeping out' a two dimensional object inspacetime. It is perhaps more accurate to think of the rod as fundamentallytwo dimensional and we experience seeing one dimensional 'slices'of the rod at any one time (see the above diagram).
For the rest of these notes, I am onlygoing to think about objects that are like points in our threedimensional space. Though we say that these points are zerodimensional objects in three-space, like the rod they 'sweep out'one dimensional lines on our spacetime diagram. Try to visualizethe appropriate spacetime diagram before you go on.
We can now think about how motion of ourpoint looks on a spacetime diagram. Let's imagine our pointstarting at the center (so that the x coordinate and timecoordinate are zero) and moving steadily to the right. After acertain time, say three seconds, the point will be off to theright. This is an event in the upper right section of thediagram. After a later time we will have another event with thepoint further to the upper right. Further, all positions of thepoint in spacetime will form a line of events. Because the motionis steady, this line will be straight. Because the point ismoving towards the right the line will be tilted towards theright:
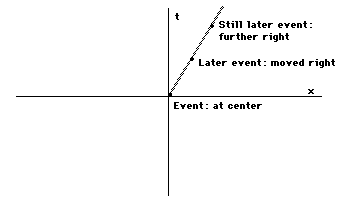
What would happen if the point weremoving towards the left? What if it started somewhere besides thecenter? Try to see the appropriate diagrams before moving on.
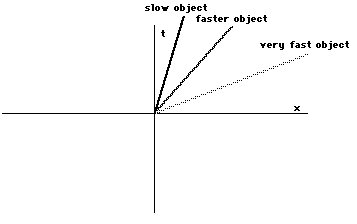
The line swept out by our point iscalled the world line of the point. What would the world line ofthe point look like if it were moving slower or faster? It wouldbe like this:
Summary:
It is natural, though strange at first,to think of time as a fourth dimension. It is not equivalent tothe three spatial dimensions. One way this shows up is that wecannot stop moving through time.
What would happen if the point weremoving towards the left? What if it started somewhere besides thecenter? Try to see the appropriate diagrams before moving on.
On a spacetime diagram, an object hasone more dimension than we are used to. A point (zero dimension)in three-space looks like a (one dimensional) line in spacetime.A rod (one dimensional) in three-space looks like a (twodimensional) area in spacetime.
A steadily moving point (in three-space)looks like a tilted straight line on a spacetime diagram. Thefaster the motion the greater the tilt.
We are now going to look at what thestatement "motion is relative" looks like in terms ofspacetime diagrams. Let us imagine two spatial points. For thesake of brevity, I will call them me and you, taking advantage ofthe appropriate pronouns. Let's say that I am standing still, andyou are steadily moving right:
• (me standing still) •»» (you moving right)
What will this look like in a spacetimediagram? Since I am watching you move, I will put myself in thecenter of my diagram. As I am not moving in space, my world linewill stay at x coordinate = 0, so my world line will coincidewith my time axis. Your world line will be tilted towards theright:
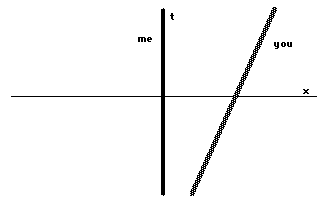
Now I decided that it is you who ismoving. This is perfectly natural, since I am sitting watchingyou move along. Perfectly natural, that is, if you are me.However, you are not me (by definition), and so to you it wouldbe natural to say that you are standing still and Iam moving towards the left:
««• (me moving left ) •(you standing still )
The situation has not changed!Physically, these two situations are the same. We have onlyshifted our point of view! What does the spacetime diagramlook like for this point of view? First, it is only natural thatyou would put yourself at the center of the diagram. I would beto the left of you. As I am, relative to you, moving steadilyleft, my world line will be a straight line tilted towards theleft:
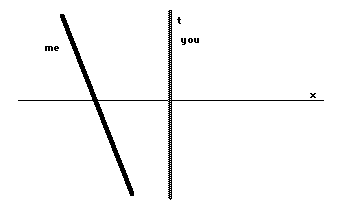
As a final exercise in the relativity ofmotion, think about the situation where you are steadily movingrelative to me towards the right as above, and a third point,named her, is steadily moving towards the right relative to mefaster than you. Then in my point of view your world line istilted towards the right and her world line is tilted more thanyours to the right. You, however, see your world line asvertical, mine as tilted towards the left and hers tilted towardsthe right, but less than I saw hers tilted:
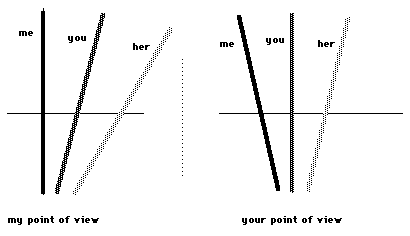
my point of view: •(me ) •»» (you ) •»»»» (her ) --- your point ofview: ««• (me ) • (you ) •»»
Try to draw the spacetime diagram fromher point of view.
Thus we see that the tilt of world linesthat we see will depend on our own state of motion. To get ahandle on the above situation, translate it into statements aboutwho is moving what direction relative to and faster than whom.
What if she were a light ray? Then thestatement "light travels at a constant velocity" wouldimply that no matter whose point of view you took the world lineof the light would be tilted the same. This contradicts theanalysis above. Resolving this conflict will give us the SpecialTheory of Relativity! This is what we do next time.
Let us look a little more closely at theabove analysis of the relativity of motion. When we were making aspacetime diagram from my point of view, we had my world linecoinciding with my time axis. This is a natural thing to do--itis the same as saying that I am always at my own position (my xcoordinate is zero relative to myself). It also says that Imeasure my own time. After all, if I carry a watch with me, I amperfectly justified in using the ticks of this watch to measuremy time. So taking my time axis to be along my world line isnatural for several reasons.
Now from your point of view, for thesame reasons given above (with you replacing me), your time axiswill coincide with your world line. But your time axis is tiltedrelative to mine--We do not have the same time axis and so wewill not measure time the same!!! In fact, I can ask whatyour time axis will look like from my point of view. In myspacetime diagram your time axis is given by your world line:
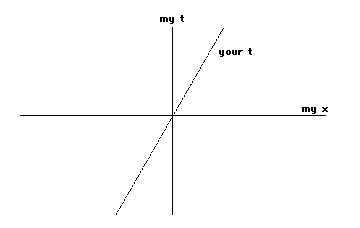
Our time axes do not (and cannot)coincide so long as you are moving relative to me. This meansthat you and I will measure time differently! This bearssaying again.
Because you and I each carry our owntime axes with us, and because when you move relative to me yourtime axis rotates relative to mine, we will measure timedifferently.
This is the insight behind so-calledtime dilation, or the fact that if you move relative to me wemeasure time differently. (Caution--It is not true that wemeasure the time of all things differently, only those that arein relative motion to you and in a different motion relative tome.)
At this point, we have only found thatif you are moving relative to me we will measure timedifferently. We do not know enough to estimate the nature of thisdifference (slower, faster, whatever). Getting actualquantitative results will require more thinking. (In particular,you do not just try to draw equally spaced timing marks alongboth axes and somehow project. This will give an incorrectanswer). I will now give an outline of what we will do in thenext session in order to do this.
We know that your motion makes your timeaxis rotate from my point of view. We need to know what happensto the x axis--Does it rotate by the same amount, not rotate atall, or something else.
We will answer this question about the xaxis by appealing to our demand that the speed of light be aconstant from all points of view. We will find that if the x axisrotates backwards from what we would expect then we havethe speed of light remaining constant from all points of view.
This strange behavior of the x axis willbring us to seeing motion as a rotation of our coordinate axeswhich is different from rotations we are used to in three-space.Just as rotation in three-space preserves the distance betweentwo points (this distance is the same no matter how you rotate inthree-space), this new kind of rotation defines a new kind ofdistance which is preserved under these new rotations.
This new kind of distance will allow usto make quantitative estimates of how we observe space and timedifferently if we are in relative motion (though we will observespacetime to be the same), and will give us the Lorentztransformation (the equations that tell us how our views of spaceand time are related).