by Steve Bryson
We have discovered that time cannaturally be thought as a fourth dimension, and that if you aremoving relative to me then your time axis appears rotatedrelative to mine. This will mean that you and I will measure thetime coordinates of an event differently. We now ask severalquestions:
What happened to yourspace (x) axis?
How is this rotationrelated to rotations in three-space?
How does this all fit inwith "The speed of light is a constant!!!"?
What are the quantitativeimplications of this rotation (exactly how do our measurementsdiffer)?
It will turn out that the first threequestions will be answered together, and the last question willonly be answered in a technical appendix. We will here beconcentrating on the first three questions.
Our path to an answer to these questionswill be to define what happens to the x-axis so that thespeed of light will be the same in all coordinates, rotated ornot. This will force us to treat the rotation of coordinates dueto motion differently from rotations in three-space. In order todo this we need to be more clear about how to represent themotion of light on our spacetime diagrams.
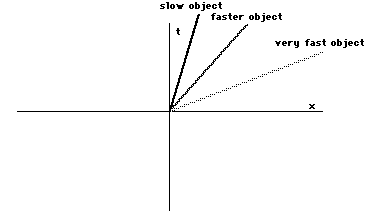
Think back to our point moving steadilyfrom left to right in our spacetime. On our spacetime diagramit's world line looked tilted, and the faster it moved the moreit was tilted:

We need a way to measure the tilt of theline, in order to translate the demand that 'the speed of lightis a constant!!!' into our spacetime diagram. We will measure thetilt of the line in the following way. If the line passes throughthe center (origin) of our coordinate axes, then here is how youmeasure the tilt: Pick any point on the line. On our spacetimediagram the point (an event) will have coordinates given by thetime and the x position. Then simply divide the x coordinate bythe time coordinate:
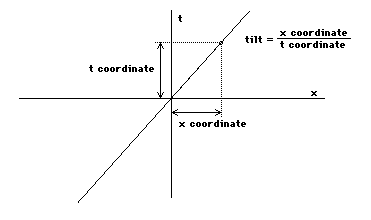
Then we have a numerical measurement ofhow tilted the line is. It is defined in such a way that a lineat 45 degrees will have a tilt of 1, as then the t coordinatewill equal the x coordinate.
Comments: The tilt as I amdefining it is the inverse of the slope of a line that youlearned about in high school geometry. I am using the inverse inorder to be more intuitive--the greater the speed of motion thegreater the tilt. In fact, as speed is distance traveled dividedby the time it took to travel, the tilt as I've defined it isthe speed of the moving point. (For those of you who know thedifference, it is actually the velocity, as it carries the propersign and so indicates direction as well as speed.) Finally, someof you may be bothered by the fact that the time coordinate andthe x coordinate are in different units (seconds and inches, forexample). As we are only interested in comparing tilts ratherthan calculating them, This is OK so long as we don't change theunits we are using. In any case, we will soon start measuringtime in units of distance anyway.
So from now on we can think of the tiltof a line as given by it's velocity. We are now in a position tothink about light.
We can now ask "what does a beam oflight look like on our spacetime diagram?" This is a subtleenough problem that it deserves it's own section.
This question already gets us in troublebecause a beam is a three-dimensional object. In order to putlight on our spacetime diagram we need to think in terms of aflash of light that acts like a point in our one spatial (x)dimension. So for now, when I say 'light', I mean a point movingat the speed of light. Think this: That point on the x axis litup by the passage of a flash of light.
So let's put this moving point of lighton our spacetime diagram. What does it look like? Like any pointmoving in a spatial direction, it looks like a tilted line on ourspacetime diagram. Let's say it's moving from left to right andgoes through the origin of our coordinates. Then the only thingwe need to know is the tilt of the world line. This is given byit's velocity, and if we are measuring time in seconds and thespatial part in inches, then the velocity of light is about11,802,852,680 inches/second. This is quite a tilt! Here's whatit looks like on a spacetime diagram.
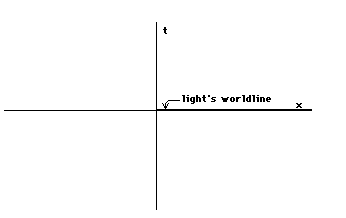
It's tilted so much that we cannot, onany diagram at a reasonable scale, distinguish light's world linefrom the x axis. Yet light's world line does not coincidewith the x axis, it is just very tilted.
We need to think about the motion oflight, and this way of measuring tilt does not help us. There isa way out. We can use our freedom of defining our units ofmeasurement to make the tilt more reasonable. After all, we donot have to measure things with inches and seconds! We could usemiles and hours, meters and minutes, or furlongs and fortnights.It turns out that no matter what units we choose, if we chooseunits that are in our everyday experience the speed of light(=tilt of light's world line) will be very large. This is simplybecause compared to things in our everyday experience light isvery fast.
So if common units do not help us, letus make up our own. At the risk of being conservative, I wish togo on measuring spatial coordinate in terms of inches. I will nowchoose a new unit of time so that the tilt of light's world lineis a reasonably visualizable one. Now I can choose this tilt, asI am making up my time unit. What tilt do I want? What can bemore reasonable than a tilt of 1? I do this by simply taking myold time unit and multiplying it by the speed of light, measuredin the old units. Lets say that my old units were inches andseconds:
New time unit=seconds multiplied by11,802,852,680 inches/second.
What kind of unit is this? It is secondsmultiplied by a whole lot of inches divided by seconds. Theseconds cancel out, and the new time unit is 11,802,852,680inches! We are now measuring both time and spatial directions ininches, though with a very different scale in the two directions.Let us adjust the scale on the x axis, so that one x unit is11,802,852,680 inches. We are still measuring spatial distancesin inches, but now one mark is not one inch, but 11,802,852,680of them.
What is the tilt of light's world line?Because light travels at 11,802,852,680 inches/second, it willtravel 11,802,852,680 inches in one new time unit (I defined thenew time unit so that this would be true). Thus in the new units,the speed of light is exactly 1, and so it's tilt is exactly 1:
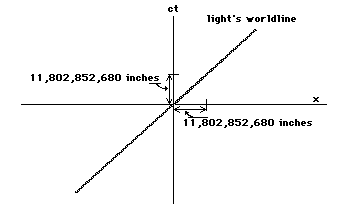
Let us give the new time unit a newlabel that will constantly remind us of how it is defined. It isdefined as seconds multiplied by the speed of light. Now I amgetting tired of writing 'the speed of light' and 11,802,852,680inches/second again and again, so let me denote the speed oflight by the letter c. Then my new time coordinate will bedenoted by ct. In this way we will never forget how this new unitwas defined.
All this was, admittedly, very dry andtechnical, but it has left us with a very easy way to visualizethe motion of light on our spacetime diagram. Light's world lineis tilted at 45 degrees. We now have a new way of saying"The speed of light is a constant!!!": "Light'sworld line has a tilt of 1 (is tilted at 45 degrees) in allcoordinate systems!!!". This second phrasing will give us aprecise way of finding it's implications.
We can now turn to the question of howyour x axis changes when you are moving relative to me. We willuse the demand that the world line of light have a tilt of 1 ineveryone's coordinate system.
Let us recall the example at the end ofthe last handout, where you were moving relative to me, and therewas a third point called her moving relative to both of us. Fromour two points of view our spacetime diagrams looked like this:
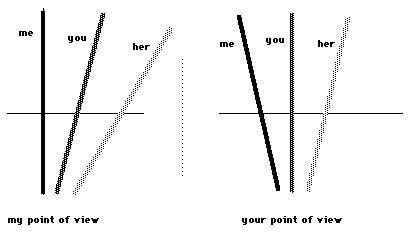
Now let's see what happens if we replaceher by light. Then according to our demand, the world line of thelight must at the same tilt in our two spacetime diagrams:
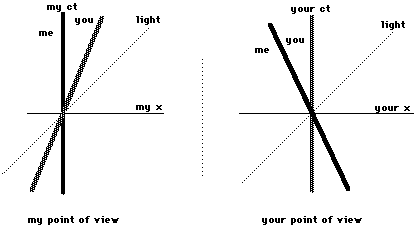
The tilt of your and my world line aredifferent in the two diagrams but the tilt of the light's worldline remains the same. This is different from the above example.
How can this be? To me, your world linemakes a smaller angle with light's world line than my world linedoes. Yet in your diagram, your world line makes the same anglewith that of light as mine did in my diagram. This is a seemingparadox.
Let us look more closely at the idea oftilt. Very picturesquely, the tilt of a line measures how closethat line is to one axis compared to how close it is to the otheraxis. By how close, I mean the angle between the line and theaxis. To say that a line has a tilt of 1 is to say that the anglethat line makes with one coordinate axis is the same as the angleit makes with the other. Thus if as your world line tilted in myspacetime diagram taking your time axis with it your x axistilted towards the world line of the light by the sameangle as your time axis tilted down, the world line of the lightwould still make the same angle with each axis! The tilt of thelight's world line would still be 1:
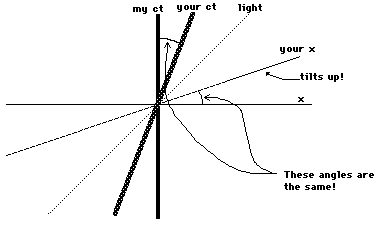
If your x axis tilted towards the worldline of the light the same amount as your time axis tilted down(also towards the world line of the light) due to your motion,then I would see that the world line of the light has a tilt of 1in your coordinate system. In other words, in order for light tohave the same speed for all moving observers ("The speed oflight is a constant!!!"), the x axis rotates backwardsfrom what would be expected given the rotation of the time axis.
This type of rotation is called TheLorentz Transformation or Lorentz Rotation.
Rotations:
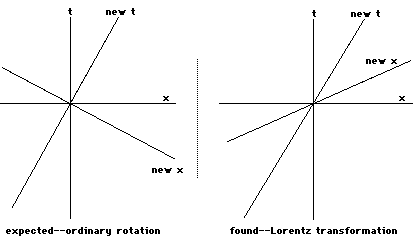
This answers the question 'How is therotation due to motion related to spatial rotations?'. It isrelated, but different.
You may have many objections to this.Remember that we are trying a point of view, and we will findthat this point of view matches well with experiment. One of thefirst objections that comes up is that if you are moving relativeto me, your coordinate axes are not perpendicular from my pointof view. This is correct, but in your point of view they areperpendicular, and so there is really no problem.
We thus now see that both yourtime axis and your x axis rotate from my point of view if you aremoving relative to me. This means that you will measure the timeand spatial coordinates of an event differently from me.
A summary of where we are is called forhere.
1) We have found that if you are movingrelative to me, your world line is tilted compared to my worldline in spacetime, that is to say from my point of view.
2) We have, from the principle ofrelativity and the laws of electricity and magnetism that thespeed of light is the same for all observers, moving or not. Thismeans that the world line of a light beam will be tilted the samefrom all points of view.
3) We recognize that your time axis,that is to say the direction in spacetime defined by your timecoordinate, always coincides with your world line, and so istilted relative to mine. This means that you and I will givedifferent time coordinates to an event.
4) In order for the world line of lightto have the same tilt in both our diagrams and to be consistent,as your time axis tilts towards the world line of light, your xaxis also tilts towards the world line of light by the sameamount.
5) This means that you and I will givedifferent spatial coordinates to an event.
And so we have that if you are movingrelative to me, you and I will give different coordinates to thesame spacetime event.
Thus the space and time coordinates ofan event are relative to our state of motion.
This is the sense in which this is atheory of relativity.
As I mentioned in the first session, theSpecial Theory of Relativity is also a theory about what isabsolute in spacetime.
Though space and time taken separatelyare relative to our state of motion, the spacetime of which theyare parts does not depend on our state of motion (oranything else about how we observe it).
Or, to quote Hermann Minkowski,
"Henceforth space by itself, andtime by itself, are doomed to fade away into mere shadows, andonly a kind of union between the two will preserve an independentreality."
Spacetime is that union. How do we seethis? What aspect of spacetime can we use to appreciate that itis spacetime that is left absolute? In order to find a thing tofit this, let us think about rotations.
The Lorentz transformation is, as I saidabove, a rotation in spacetime. It is, admittedly, different fromthe rotations we are used to, but it is (especially whenexpressed mathematically) the same kind of animal. Let ustherefore think a bit about more 'normal' rotations.
Here is a purely spatial rotation of xand y axes:
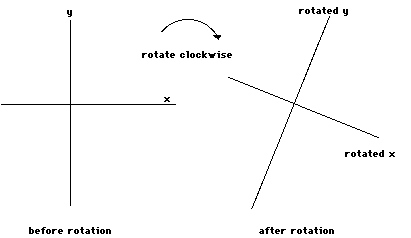
We can superimpose the before and afterpictures to get a way to compare the two points of view:
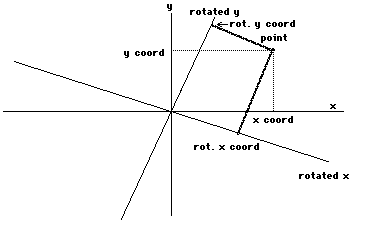
Now the x and y coordinates of a pointare going to depend on whether they are measured from theunrotated axes or from the rotated axes. To say it another way,the distance of the point from each axis depends on whether ornot the axis is tilted. The coordinates of the point are relativeto the orientation of the axes--it is as simple as that.
There is, however, something that is thesame when measured with both coordinates: The distance of thepoint from the center of the axes. It doesn't matter how you tiltthe coordinates, how far the point is from the center does notchange. Why is this so? Because you did not move the point orthe center when you rotated the coordinates. If neither pointmoved, how can the distance between them change?
The simplest way to express thisdistance is by measuring it with a ruler. This does not help us,though, as we wish to generalize this to spacetime, and there areno spacetime rulers that you can hold in your hand. We can,however, express this distance in terms of the coordinates of thepoint. The distance is given by the formula:
distance = square root of(x coordinate times x coordinate plus y coordinate times ycoordinate)
Yes, this is mathematics, but we willsoon get used to it. First let's write it in a more convenientway. I want to write x for x coordinate and y for y coordinate.Also I will write x2 for x times x and y2for y times y Then the formula looks like:
distance = square root of(x2+y2)
Finally, I will write d for distance,getting d = square root of (x2+y2). Now itis clumsy to carry the phrase "square root of" all thetime, so I will simply square both sides, in order to write theformula in the equivalent form:
d2 = x2+y2
This is the formula for the distance ofa point from the center of the coordinate axes in terms of thecoordinates of that point. It will give the same number d2no matter how you rotate the coordinate axes. This is aremarkable fact, for the values of x and y will be different ifyou rotate your coordinates. This formula is special in that thedifferences exactly cancel out--the x gets a little biggerperhaps and the y gets a little smaller, so that if you add themtogether the differences cancel.
Now we are viewing the Lorentztransformation as a rotation in spacetime. Is there a spacetimedistance formula that takes x and ct (the new time coordinate)and produces a distance that does not change under Lorentzrotations? Let us call the spacetime distance s. It turns outthat the formula s2 = c2t2+x2changes under Lorentz rotations. Therefore it cannot be thecorrect formula for the spacetime distance of a point (event)from the origin.
There is, however, a formula that doeswork. Here it is:
s2 = c2t2-x2
It is the same as the other distanceformula, except that instead of adding the squares of thecoordinates, you subtract them. The reason for this is that arotation in spacetime is different from a spatial rotation. Thisdifference is completely described by this distance element. Allof this will be covered in a soon to arrive technical handout.
This distance formula is indeed the sameno matter how I rotate my axes in spacetime, using Lorentzrotations. Let me say this in a technical way. Let x and ctdenote my unrotated coordinates, and x' and ct' denote yourrotated coordinates. Then:
c2t2-x2= c2t'2-x'2
Thus though you and I will measure thetime and spatial coordinates of an event differently if you aremoving relative to me, there is something we can agree upon, thespacetime distance.
Using this distance formula, we canderive formulas for the quantitative difference between our timeand space measurements. We find that if you are moving relativeto me and you say that an event has coordinates x' and ct' then Iwill see that the same event has my coordinates x and ct given by
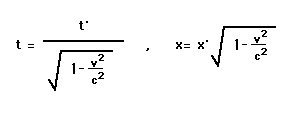
This will be derived in the technicalhandout.
This completes our visitation with thefoundations of the special theory of relativity. Next time wewill look at all the implications of the Lorentz transformation.