by Steve Bryson
We now have our spacetime diagram, a wayof visualizing spacetime. We know how to express our both owncoordinates on it and the coordinates of someone moving relativeto us. In a spacetime diagram, we have our own coordinatesrepresented by two perpendicular lines:

In our spacetime diagram, the coordinateaxes of someone moving relative to us will look like two linestilted towards each other, and the faster the motion the moretilted towards each other they are. Call the moving coordinatesx' and ct':
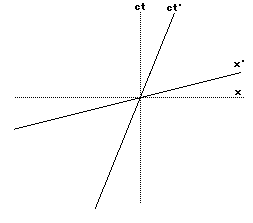
Remember that the reason for this funnytilt is so that the speed of light will be the same for allobservers. Now we want to ask how to compare actual measurementsin the two coordinate systems. In other words, we are asking thequestion "given an event with coordinates ct and x in mycoordinates, what will it's coordinates ct' and x' be for someonemoving relative to me?" We can visually find the ct' and x'coordinates on our spacetime diagram by using the followingsimple rules:
To find the ct' coordinate of an event,draw a line parallel to the x' axis through the event. Where thisline meets the ct' axis is the ct' coordinate of the event.
To find the x' coordinate of an event,draw a line parallel to the ct' axis through the event. Wherethis line meets the x' axis is the x' coordinate of the event.
So here are two diagrams showing how tofind the ct' and x' coordinates of an event:
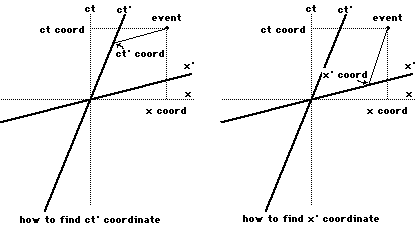
Here we can see that if an event takesplace at, say, ct = 1 then in the moving coordinate system, theevent will have ct' less than 1. This means that time seems to meto be passing slower for the moving coordinate system. Similarly,if the event had x coordinate for me, then it x' coordinate willbe less than one. This means that my moving friend would thinkthat the event is not as far from the center of the diagram as Ido.
Now remember that these diagrams cannotbe used to get the actual numerical values of the ct' and x'coordinates. To do this we must use actual formulas. I will giveyou these formulas, but in this class I cannot show you why theyare true. That is the material for a technical handout, though itwill be the easiest thing in the handout. Here are the formulas,where v is the velocity of the moving coordinates relative tomine, and c is, as usual, the speed of light:
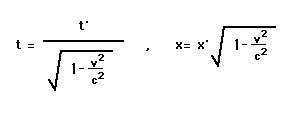
These formulas are true in all units ofmeasurements, miles, seconds, etc. If you have a calculator witha square root function, you may wish to plug in some samplevelocities and see what happens. You will discover that if v ismuch smaller than the speed of light, then v2/c2is very small and so 1 minus this is still very close to 1. Asthe square root of 1 is 1, then the factors effecting thecoordinates in the above formulas are very close to 1 and so thecoordinates are not very different. In fact, for speeds that weare used to, the difference is entirely undetectable. This is whywe do not have an intuitive feel for relativity.
Let's now see what this all means. Weneed to look at a case where you will go on a trip and travel atsome speed close to the speed of light and go a very greatdistance. In this way, the difference in coordinates between uswill be large enough to appreciate.
Say that you needed a real change ofscene and decided to fly to the star Alpha Centauri, this beingthe nearest star. Even though this is the nearest star it isstill quite far away, at a distance of 4.3 light years(=25,277,980,000,000 miles), and so you choose to travel at 90%of the speed of light, or at 167,654 miles per second(603,554,400 miles per hour). Let's say that you accelerated atthis speed in an instant of time, not worrying about how you didthis or whether or not you could survive this acceleration. Thenthis is what the situation would look like on my spacetimediagram:
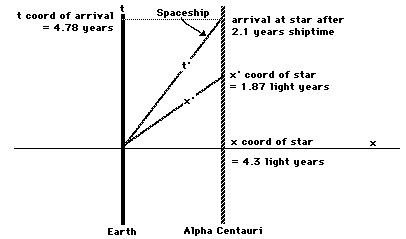
We see that while you arrive at the starafter 4.78 years have passed for me, the time that passed for youwill be much shorter! (In evaluating the above diagram, there isa subtlety in that here we are noticing what you would say thetime on Earth is on your arrival.) In fact, the time that passesfor you is only about 2.1 years. This is because at this speedthe conversion factor in the above formulas is only about .436,and .436 times 4.78 years is about 2.1 years. Thus you would saythat you arrive at Alpha Centauri after only 2.1 years of travel.If you immediately took off again and flew back to Earth at thesame speed, only 4.2 years would have passed for you while for me9.56 years would have passed. Thus I would have aged 5.36 yearsmore than you since we last met! This is a very physical resultof living in spacetime.
What if I managed to take a picture ofyour spaceship as you flew by at 90% of the speed of light? Let'ssay your ship is a mile long, so that if you orient yourcoordinate system so that the tail of the rocket is at yourorigin then the nose will have x' coordinate = 1 mile. For me,the x coordinate of the nose of your ship will be at 1 mile times.436 or at .436 miles. Your ship would appear shorter to me bymore than half!
In fact, you would see both the Earthand Alpha Centauri moving at 90% of the speed of light, and sothe distance between them would seem to be 4.3 light years times.436 = 1.87 light years. This is exactly the distance you thinkyou would travel at 90% of the speed of light in 2.1 years, andso everything looks perfectly natural to you. This is thesituation from your spacetime diagram:
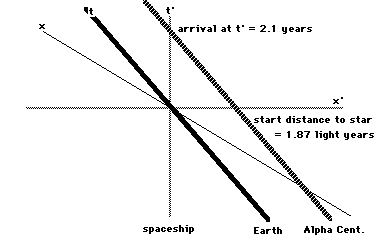
So to me, you traveled 4.3 light yearsin 4.78 years traveling at 90% of the speed of light, but youonly aged 2.1 years. To you, you traveled 1.87 light years at 90%of the speed of light and so you aged 2.1 years, exactly how longsuch a voyage should have taken. The unusual thing for you isthat the distance you had to travel was much shorter than youthought it should be.
But wait! If you are moving relativeto me then I am moving relative to you!
Why don't the effects exactly cancelout?
If you flew to Alpha Centauri as in theprevious section and flew back again, then you would age 4.2years and I would age 9.56 years. Yet we have been saying allalong that motion is relative--who is to say whether it was youmoving or if it was I? This is known as the twin paradox, as itis commonly stated with regard to comparing the ages of twins.
In fact, it is not a paradox at all, forit involves a confusion about the statement "motion isrelative". While it is true that steady motion is relativeto the person observing the motion, acceleration is not. When youaccelerate, you cannot close your eyes and pretend that nothingis happening. You will feel the acceleration, and you can doexperiments, such as watching a hanging string, which measureyour acceleration and do not refer to other observers. So if youtake off in your rocketship, you must accelerate (in our exampleinstantaneously) and this makes your situation different frommine in an absolute way. The exact difference is in the rotatingof your coordinate axes by the act of acceleration. When you turnaround to come back, you undergo another acceleration whichcauses your axes to 'swing around' and in so doing you do notexperience as much time as I do. This can be understood bycarefully staring at the following spacetime diagram:
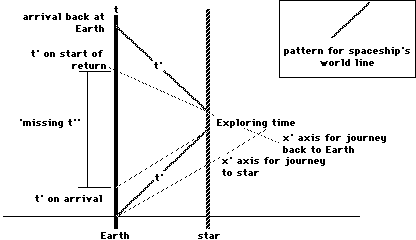
If, on the other hand, you just happenedto be going at 90% of the speed of light relative to me and didnot speed up or slow down, then our situations would be reflexiveand the effects would exactly cancel. I would think that time waspassing slower for you and your objects were flattened, and youwould think it was I who was flattened and my time that wasrunning slow. We could not, however, ever compare ourobservations without agreeing on a coordinate system, and wecannot do this without one of us accelerating. That would destroythe symmetry of the situation.
The twin paradox is an excellent objectlesson that one must be very careful about how one interpretsthings in spacetime.
More on thespacetime distance
Remember the spacetime distance, labeleds from the last session? It represents the distance of an eventfrom the origin, and in terms of coordinates it is given by theformula
s2 = c2t2- x2
This distance has a special property,that it is the same in all coordinate systems. It has tremendoussignificance for what happens in spacetime, and in fact you canstart with this formula for the distance and derive all ofrelativity theory (this is the way that I actually approach thesubject). We will only mention a few aspects of this distancehere.
First, what is the spacetime distancefrom my origin to a point on my world line? Any point on my worldline will have a time coordinate t given by the time that passesfor me, and an x coordinate with the value zero (it is where Iam). So the spacetime distance is given by
s2 = c2t2- 0
= c2t2
so that s = ct. This means that for me,the spacetime distance is simply the time that passes for me.That is to say that the spacetime distance between two events onmy world line is given by the time that I would say passedbetween the two events. This is true only for events on my worldline.
We can use this to quickly analyze thesituation from above where you flew to Alpha Centauri at 90% ofthe speed of light. Here we are interested in the spacetimedistance between two events, your launch and your arrival at thestar. The first event is at the origin of both of ourcoordinates, so they have coordinates t = t' = 0 and x = x' = 0.The second event is given in my coordinates by t = 4.78 years andx = 4.3 light years. We want to find the coordinates of thesecond event (your arrival) in your coordinate system. Weautomatically know the x' coordinate-- it is zero (you arrivedthere). Thus all we have to do is plug my coordinates into thespacetime distance to get (because we are measuring distance inlight years the speed of light c = 1):
s2 = t2- x2
= (4.78)2 -(4.3)2
= 4.36
= (2.1)2
= t'2
So we see that you will arrive at thestar after 2.1 years had passed for you. Using this method wehave seen that time passes slowly for you without actually usingthe coordinate transformation formulas at the beginning of thishandout.