by Steve Bryson
We have been using, as a starting pointfor this course, the (God given) principle that "The speedof light is a constant!!!". We have derived the form of theLorentz Transformation from this principle in combination withthe insight that we live in a four-dimensional spacetime. Thisprinciple has other implications, and here I want to examine oneof them.
If the speed of light is constant forall observers, then by moving you can never go faster than thespeed of light, as this would mean that in some way you 'caughtup' with the light. You can hardly do this if the light is alwaysgoing the same speed of light relative to you. Thus inprinciple you can never go faster than the speed of light. Ithas nothing to do with engineering requirements or some othertechnical aspect of how you move.
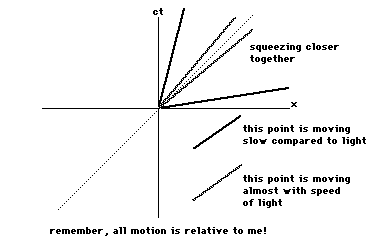
In spacetime diagram terms, we expressthis by saying that your world line can never have a tilt greaterthan that of the world line of light. In our special coordinatesthis means that your world line can never have a tilt greaterthan 1.
The principle that gives you this canactually be seen by looking at how the coordinate axes of amoving coordinate system tilt in your spacetime diagram. Thefaster the motion, the closer to each other the coordinate axesget, until at the speed of light they meet. The moving time and xaxes merge into one. This is referred to by physicists as acoordinate singularity. It is not always a bad thing to havethese singularities, but it does indicate that something funny isgoing on. In this case, it is felt that starting with twoseparate dimensions and collapsing them down into one issomething that the world does not do.

The first real objection to all thisrelativity stuff is not the twin paradox, but rather the problemof addition of velocities. Consider this scenario: I am flyingalong at 75% of the speed of light relative to Earth and I launchyou in a rocket at (relative to me) 75% of the speed of light.Then, you may immediately ask, wouldn't you be going at75%+75%=150%=one and a half times the speed of light relative toEarth? This of course contradicts the principle that you cannever go faster than light in any coordinate system, andtherefore indirectly contradicts the principle of relativity!
The resolution lies in looking carefullyat how velocities in different coordinate systems add. It turnsout that you do not simply add the two velocities together.Instead you use a somewhat more complicated formula. If v1, v2,and v3 are your velocity relative to Earth, my velocity relativeto Earth, and your velocity relative to me then the formula forthe addition of velocities is:
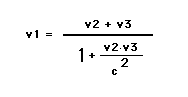
In the above example, you end up going96% of the speed of light relative to Earth. If you look at thisformula, you will find that it can never have a value greaterthan the speed of light so long as each velocity is less than thespeed of light. It turns out that this funny formula for additionof velocities comes very naturally from treating motion as arotation in spacetime.
If we cannot go faster than light, thenwe cannot get places as fast as we might like to go. As AlphaCentauri is 4.3 light years away, I cannot get there in less than4.3 years Alpha Centauri time (even though I may experience ashorter travel time). Thus if I found out that there was going tobe a convention of relativity teachers there next year, no matterhow hard I tried I could not make it. I would arrive there toolate to participate. In particular, I could not causally effectwhat happened there. I could not even send a message, for lightwould take 4.3 years to get there, and nothing goes faster thanlight. This is an event in spacetime that I can have nothing todo with. There are many such events.
It is easy to characterize these events.They are all events that are far enough away from me so that Iwould have to travel faster than light to get to them. Inspacetime diagram terms, they are all the events such that if Idrew a line from me to them (that is to say from my world line atthe time I start to travel to these events) the tilt of that linewould be greater than one. This also covers all the events that Icould send messages to, as the world line of the medium of themessage must also have a tilt less than one.
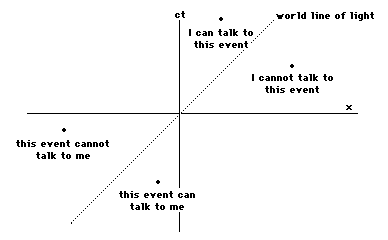
All this also applies to my past (eventswith my time coordinate less than zero), as they cannotcommunicate with me faster than the speed of light.
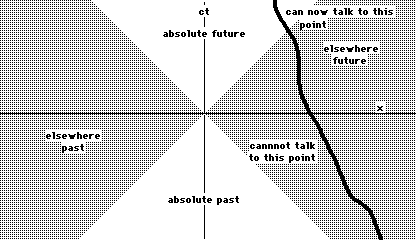
On our spacetime diagram, it is thuseasy to tell what parts of spacetime we can have anything to dowith. To find out if you can have interaction with an event, drawa line from your origin to that event, and then if that line hasa tilt less than one you and the event can talk. (It can talk toyou if it is in your past and you can talk to it if it is in yourfuture.) The boundary between events that you can communicatewith and those you cannot is the two lines with a tilt of one(one in each direction). These two lines are the world lines oflight going in two directions, and these lines (this boundary)are called the light cone of the event. It is called a conebecause in three dimensional spacetime it actually forms a cone.
We call the set of events that we cancommunicate with inside the light cone and those events that wecannot communicate with outside the light cone.
Those events that have my timecoordinate greater than zero and are in my light cone are trulyin my future, no matter how I move. Similarly, those events withtime coordinate less than zero are in my past. Thus even thoughmy time measurements of events are relative to my state of motionrelative to them, their being in my future or past is not. Thisis safeguarded by the speed of light being constant for allobservers.
Similarly, those parts of spacetime thatI cannot communicate with are not relative to my state of motion.Thus spacetime is split into sections:
For us, living and experiencing athree-dimensional space in time, the idea of velocity is anatural measure of motion. Velocity is given (in terms ofcoordinates) by x/t, where x is the distance traveled and t isthe time it took to travel that distance. In spacetime, however,x/t is not the velocity but the tilt of the world line. What canwe say about a spacetime version of velocity? In other words, howdo we generalize the idea of velocity to four dimensions?
Let us look more closely at thedefinition of velocity as x/t. This is taking the distance anddividing by the time--it assumes a difference between space andtime, giving time a privileged position. The whole idea ofthinking in spacetime is to say that time is not an inherentlydifferent direction. Thus, time should be in the top of theequation as well as x. In other words, we want to think in termsof velocity in the time direction as well as in the x (or y or z)direction. This is treating space and time as the same kind ofthings.
What do we put in the bottom of thedefinition then? It should be something that matches our sense ofvelocity as x/t, so that we recover our usual sense of velocityfor small velocities. In particular, for us in our own coordinatesystems whatever we put in the bottom should be equal to our timecoordinate, yet it is not our time coordinate. What do we knowthat does this?
The spacetime distance does this. Recallfrom last time that the spacetime distance s from our origin to apoint on our world line is just our time coordinate t of thatevent. This is the same as saying that in our reference frame thespacetime distance is just the elapsed time (= the timecoordinate).
Thus we take as the spacetime velocitydirection/(spacetime distance). So the time velocity is given byt/s, the x velocity is x/s, and so on. How is this related to thethree-space velocity (=x/t) that we are used to?
First, in our reference frame, s=t forus, so our spacetime velocity in the t direction = t/t is exactlyone (we are always moving through time at a speed of 1 (=thespeed of light) relative to ourselves!).
For velocities of objects movingrelative to us with (three-space) velocity v = x/t, we have thattheir spacetime velocity in the x direction is given by
x/s = x/t times t/s
= v times the spacetimevelocity in the t direction.
So we only need to know the spacetimevelocity in the time direction. As is shown in the first part ofthe technical handout, this is given by:
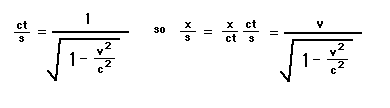
This is going to be very important inthe next section.
We need to get a little technical here.There are these two things that physicists like to think aboutquite a lot. They are called energy and momentum. These twoquantities are special to physicists because in most interactionsof objects they are conserved. We speak of the observedfacts of conservation of energy and conservation of momentum.
I wish to talk about conservation ofmomentum for a while. Momentum is a way of measuring the amountof motion that a body has. By saying that momentum is conserved,I mean that if you take a physical system, add up the momentum ofall it's parts, then later no matter how the momentum of theindividual parts have changed, the momentum of the entire systemwill be the same. This makes momentum very dear to physicists asit allows them to calculate all sorts of things about theinteractions in the system.
In old fashioned three-space plus timeNewtonian physics, momentum, denoted by p, was given by theformula p = mv where m is the mass and v is the (three-space)velocity of the object we are interested in. For low velocityinteractions (the only kind that physicists saw until about 60years ago) this quantity was indeed conserved.
When relativity came on the scene,however, it became clear that p = mv will not be even vaguelyconserved in high velocity collisions. Indeed, it wasn't reallyconserved in the low velocity interactions--the violation of theconservation was just too small to measure. By doing a rathercomplicated analysis, physicists (lead by Einstein) calculatedthat there is still a conserved quantity, and it is given by:
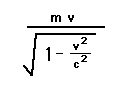
This looks a lot like the old fashionedformula for momentum, with the mass replaced by the quantity
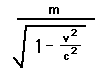
This quantity gets bigger the faster wego. This lead people to talk of the mass of an object increasingas the object went faster and faster. This lead to greatconfusion.
It is no wonder that it lead toconfusion! Here the physicists were insisting on definingmomentum in terms of the three-space velocity! Look at the newformula for the momentum above. It is just the mass multiplied bythe spacetime velocity in the x direction. So what can be morenatural than to take as the definition of momentum mass times thespacetime velocity (a four-dimensional object) rather than masstimes the three-space velocity (a three dimensional object intime)?
This means that our spacetime 4-momentumhas four parts, one for each direction in spacetime: mct/s, mx/s,my/s, and mz/s. In terms of the three-space velocity, they aregiven by the formulas (where here we are only considering motionin the x direction to that the y and z parts are zero):
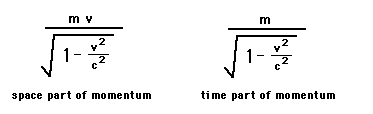
We see that the space part of the4-momentum is just the correct-that is to say conserved-3-momentum from above. What is the significance of the time partof the 4-momentum? If you are a mathematically sophisticatedperson, you try to approximate the formula for the time part ofthe momentum. If you do this you will find that you get that forlow velocities this will be equal to:
mc2 + 1/2 mv2
The second term here is just the usualthree dimensional expression for the energy of motion from oldfashioned Newtonian mechanics. The first term is completely new.It has the units of measurement that physicists use to describeenergy (mass times distance squared divided by time squared) andit is added to the non-relativistic expression for energy. Thusit is natural to assume that this is the new relativisticmeasurement of the energy of a body.
This is what physicists do. They definethe energy of something as the amount of 4-momentum that body hasin the time direction. What is the value of the energy ofsomething that is not moving relative to you? That something willhave velocity v equal to zero, so the energy E is given by theformula
E = mc2
This is one of the very few formulasthat almost everyone knows, though most people do not know whatit means. It does not mean that energy and mass are the samething. After all, if an object moves, it also gets the energy ofmotion. What it does say is that an object of a given mass has acertain (very large) amount of energy inherent in it. Actuallymanifesting this energy as energy is something that we have to gointo the realm of quantum field theory to see.
The reason that this inherent mass ofobjects was never before known is that physicists only know howto measure changes in energy. This energy due to mass neverchanges, so it was never seen.
For now, just let me say that we doindeed know how to convert a certain amount of matter intoenergy. The sun shines by converting electrons and anti-electronsinto light energy. In fact, the sun converts about 4.75 milliontons of electrons and anti-electrons into energy every second!(This amounts to about 4x1041 electrons per second.The Sun has enough electrons to do this for many billions ofyears.) This is where the tremendous amount of energy that thesun puts out comes from. This is also done in any explosion of ahydrogen bomb. It is also done rather often in an experimentalsetting Berkeley and Stanford (as well as many otherlaboratories). Because the speed of light squared is a very largenumber, a little bit of mass is worth a whole lot of energy.
Conversely, energy does have massaccording to this formula. In this sense, an object does indeedget more massive when it moves, but this gain in mass is the'weight' of the energy of motion of that object. It is notwhat physicists mean when they refer to the mass of an object.What they are referring to can be best thought of as themass-energy of an object at rest. This turns out to have a verynice geometric interpretation.
All of the above discussion on energyand momentum was unpleasantly abstract. Does it have a moreintuitive description in terms of objects in spacetime? Yes itdoes!
The spacetime 4-velocity defined aboveis truly a spacetime velocity as it measures your rate of travelalong your world line. You have a certain coordinate (in whatevercoordinate system you are using) which falls on your world line,and this coordinate changes as your time coordinate changes.
Now in your coordinate system, the timecoordinate is the only coordinate that changes-- your xcoordinate is always zero in your coordinate system. As statedabove, your spacetime velocity is always 1 and is in the timedirection. If you are moving relative to me, however, you havesome spacetime motion in both the x and the time directions. Ican compute these components of your velocity from the formulasfor spacetime velocity in terms of your 3-velocity. It turns outthat your spacetime velocity will also have magnitude 1 in mycoordinate system. In fact, it will always have magnitude 1 inevery coordinate system, though the components will be different.
Now the spacetime 4-momentum is masstimes the spacetime velocity. This is something called a vector.You can think of a vector as an arrow in our space. The length ofthis arrow will always be equal to m, the mass, and the directionof the arrow will be along the object's world line. Then when theobject is motionless relative to you, the object's 4-momentumvector will always point along it's world line. It will pointparallel to your time axis, so it will be the time component ofthe 4-momentum. There will be no x (or y or z) component.
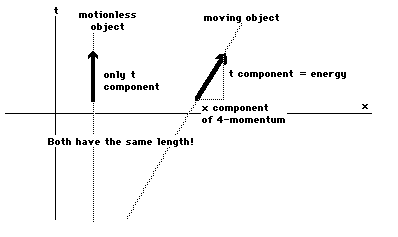
Now set the object in motion relative toyou. It's world line will lilt, and it's 4-momentum vector willalso tilt, keeping the same length (= the mass). Then you willsee both a time and an x component of the 4-momentum.
Thus the significance of the mass of anobject is, for us, that it is the length of the 4-momentumvector.
One thing about spacetime that is simplyimpossible to draw on a spacetime diagram is that as an arrowtilts, the components both get bigger. Thus as the object moves,both the time component (energy) and the x component (3-momentum)of the 4-momentum get bigger.