by Steve Bryson
The simplest quantum field theory used today is the theory ofthe interaction of electromagnetically charged particles withlight. This theory is called Quantum Electrodynamics, or QED. Itis usually used to describe the interaction of electrons withlight, as that is the most common charged particle that isobserved (When you work with the proton, you run intodifficulties because of the strong nuclear force, but QED applieshere also). QED is a gauge theory (see next week's handout), andthe force described by QED (the electromagnetic force) is said tobe carried by a particle called a photon. This photon is also tobe considered the particle aspect of light. As described in thehandout on gauge theories, the photon is, from the perspective ofgauge theories, related to how the direction of the chargedparticle's quantum wave changes from point to point. For thepurposes of this handout, however, we will be treating the photonas an independent particle.
Even though the word 'particle' is used to describe both thecharged particle (i.e. the electron) and the photon, theformulation of QED is entirely in terms of the quantum waves ofboth the charged particle and the photon. Basically, QED is atheory of how the photon and the charged particle quantum wavesinteract. It is actually rather easy to state the equationstelling everything about this interaction (once you know thelanguage, of course). These equations only tell you the nature ofthe interaction, however. In order to tell just what a particularinteraction (such as two electrons repelling each other) lookslike, you need to solve the equations of QED. This turns out tobe very difficult.
Basically the problem is that no one knows how to solve theequations of QED exactly in any but the most trivial cases. Whatis done is approximate the solution using a technique known asperturbation theory. This technique starts with some exactlyknown solution to the equations of QED which, hopefully, describea situation not too different from the situation that we areactually trying to solve. Then this first guess is refined bytaking the next most complicated situation and adding that to thefirst guess. This is done for as many stages as you wish to docalculations. To my knowledge the farthest that this has been sofar carried out in QED is four steps, as the calculation gets alot more complicated with each step.
This technique only works if the contribution from each morecomplicated situation gets smaller with each more complicatedstep. In QED this turns out to be the case, as each step getsdivided by a factor of 137*137 = 18769 for each level ofcomplication. In other words, the second step adds a contributionto the answer that is 1/18769 as large as the first step, thethird step adds a contribution to the answer that is 1/18769 aslarge as the second step and so on. Thus as you get to later andlater steps to your approximation the refinements get smaller andsmaller. Once you have gone three, or at most four steps you knowthat the difference between the real answer and you approximationare so small as to be unobservable.
Now it is true that you still do not have the exact answer.This does not mean that QED is not an exact theory. Presumably(at the distances with which QED is concerned) QED as formulatedis an exact theory. It is only that we do not have themathematical oomph needed to write down exact solutions of QED.It is only the numbers describing a particular case that isapproximately calculated.
There is one technical point involved with the calculations inQED (and in perturbation calculations in most quantum fieldtheories). If you simply calculate each step in the moststraightforward way, you find that at the second and third stepyour refinements are infinitely large. This is bad, as when youdo an actual experimental observation of the interaction that youare trying to describe there are no infinite results observed.One must resort to a technical trick called renormalization inorder to get finite numbers, and when you do you find that thenumbers that you calculate are in exact agreement with yourobservations (if you go enough steps). In a little more detail,here is a schematic version of what you find at the second stepof a perturbation calculation in QED:
First step = some finite number
Second step = another finite number + infinity
so
Two step approximation = First step + Second step
= a finite number + infinity
The finite number in the last line is the sum of the finitenumbers from the first step and the second step. The reallysurprising thing is that even though the two step approximationis really an infinite number (and therefore technically wrong),the finite number is exactly the value that you find in anobservation. In other words, if we can get rid of that infinitepart in the two-step answer then we would have an answer thatagrees with experiment.
It turns out that by very cleverly redefining the constants inthe original equations of QED one can make the infinitydisappear. The constants that must be changed are such things asthe mass and electric charge of the charged particle that isbeing acted on by the photon. You see, originally the mass andelectric charge used in QED were the ones that we observe. Itturns out that that was the wrong mass and charge to use. If wechoose our starting mass and charge just right, then the actualobserved mass and charged are consequences of the interactionsbetween the charged particle and light. This is called renormalization.It may seem that this is all some kind of parlor trick, and infact that is all it was when it was first invented (manyphysicists still feel this way). In the last decade, however, amuch clearer understanding of renormalization has emerged. Inparticular it seems that the infinities (and therefore the needto renormalize) arise from the perturbation technique and notfrom the fundamental structure of QED. In fact simple modelquantum field theories that exhibit the infinities in pertubationsolutions have been shown to be completely finite when solvedexactly.
When using pertubation techniques to solve quantum fieldtheories, there is a very convenient pictorial method ofconstructing what the refinements at each step of theapproximation are due to Richard Feynman. Let us consider thecase of the QED interaction between light and electrons. Onedraws the electron as a solid line with an arrow pointed to theright (or up):
![]()
An anti-electron is drawn as a solid line with an arrowpointed to the left (or down):
![]()
and the photon as a wiggly line:
![]()
Then the interaction between a photon and an electron is drawnas a photon line attached to two electron lines:

Note that one can think of this as an electron moving alongand interacting (either emitting or absorbing) a photon andchanging direction. The fact that this diagram is allowed isdetermined by the equations of QED. A diagram that is not allowedis one like that above with the roles of photon and electroninterchanged. This is why we say that the photon acts on theelectron and not vice versa.
This diagram connecting two electron lines with a photon lineis called a vertex. This is the only vertex allowed in QED. Notethat the arrow on one of the electron lines must point towardsthe vertex and the other arrow point away. A vertex diagram with,for example, three electron or three photon lines meeting at apoint is not allowed. Other than three lines of any kind meetingat a point is also not allowed. Once you know how to draw yourallowed diagrams, there are rules for translating the diagramsinto mathematical terms in your pertubation calculations. Inparticular, each vertex gives that term in your calculation afactor of 1/137 in QED.
Now you are ready to roll. To calculate each step in yourpertubation expansion, you draw allowed diagrams with increasingnumber of vertices. Each step in the calculation is defined asthe mathematical term given by all possible diagrams with aparticular number of vertices.
Let us look at an example of the interaction of two electrons.Other interactions would have diagrams different from thefollowing.
For technical reasons, it turns out that diagrams with an oddnumber of vertices give approximation terms that are exactlyequal to zero. Thus the simplest diagram, and therefore the firststep in our approximation, is given by all the diagrams with twovertices. There is only one of these:
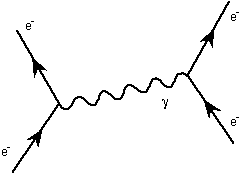
The next term is given by all possible diagrams with fourvertices, which give terms that are 137*137 = 18769 times smallerthan the first term. There are actually many of these,represented by the following:
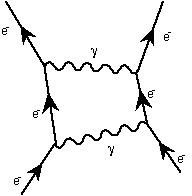

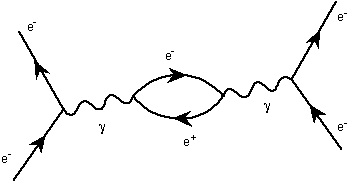
It is with these diagrams that the troubles begin. Inparticular, the diagrams with a loop in them give the infinitiesthat must be removed by renormalization. The lines in the loopsare called 'virtual particles'. Thus one can have both virtualphotons and virtual electrons. This is where the concept ofvirtual particle arose.
When you allow six vertices (third step in the approximation),things get much more difficult. Here an example:
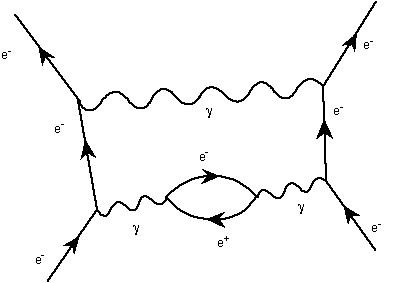
A really fun thing about Feynman diagrams is that if you haveone diagram that is allowed, then rotating that diagram by 90degrees on the paper gives another allowed diagram. For example,if you have the original vertex diagram from above describing theinteraction of an electron with a photon:
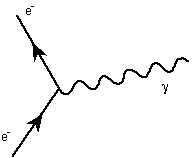
and you turn this 90 degrees clockwise, you get a diagramdescribing an electron and an anti-electron coming together andturning into light:
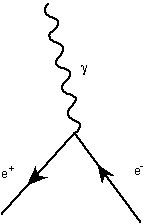
Now this diagram will actually vanish because it has only onevertex, but the following diagram showing an electron and ananti-electron turning into two photons via an intermediatevirtual electron:
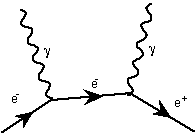
This diagram, turned 180 degrees turns into the following:
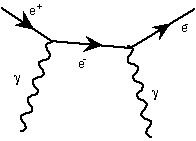
This describes two photons coming together and turning into anelectron-anti-electron pair again via an intermediate virtualelectron. Though this is allowed by QED, the chances of twophotons coming together like this is extremely low.
The next simplest theory is Quantum Chromodynamics or QCD. QCDis formulated mathematically exactly like QED except that insteadof one charge as in QED, QCD describes particles with threecharges called red, blue, and green. The three charges aregenerically referred to as color (hence the chromo in quantumchromodynamics). Particles with color are, by definition, quarks.Thus all the difficulties of QED are present with a host of othercomplications.
Not the least of these complications is the fact that when onedoes a pertubation solution of QCD each of the refinement termsat each step is not smaller than the previous step. In fact theyget bigger. This means that to get the correct answer one needsto calculate all the possible diagrams, because if you stopped atsome step, the remaining steps are at least as significant aswhat you calculated. But there are an infinite number ofdiagrams! Thus answers in QCD cannot be calculated usingpertubation techniques. This stopped progress in QCD for sometime.
There is a way out, however. It turns out that if you use QCDat very small distances (= very high energies), then the terms inyour pertubation calculation do get smaller with each step andyou can make calculations in QCD just like in QED (includingrenormalizing, of course). Thus so long as you are looking atsituations that are involving distances that are small enough(about the size of a proton), you can do calculations. If youwish to know about the behavior of QCD over larger distances(calculating the mass of the proton, for example) you are out ofluck until somebody invents better techniques (one suchtechnique, called 'lattice field theory', approximates spacetimeas being a discrete set of points and does numerical calculationsof QCD on computers). This unusual behavior of diagrams in QCDcomes from the fact that the QCD force (the strong nuclear force)gets weaker with shorter distance.
QCD has its own set of Feynman diagrams. First, the particlesinvolved are quarks and gluons (gluons are the analog of photonsand carry the QCD force). The quarks and gluons are drawn asfollows:
quark
![]()
anti-quark
![]()
gluon
![]()
Because there are three charges in QCD (as opposed to one inQED), there are more allowed diagrams. There is the basic vertexdiagram of a gluon interacting with a quark:
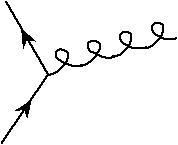
There are also new vertex diagrams that show the interactionsof gluons with themselves. The allowed ones are three and fourgluons coming together at a point:
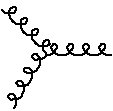
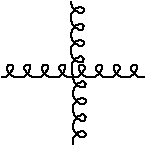
This, needless to say, makes calculations in QCD a good dealmore complicated than QED even when we can use pertubationtheory. The main thing that one finds that is of interest to usis that bound states of three quarks together andquark-anti-quark pairs are to be found in nature. This explainswhy we see the particles we see. Examples are to be found in theglossary in the first handout.